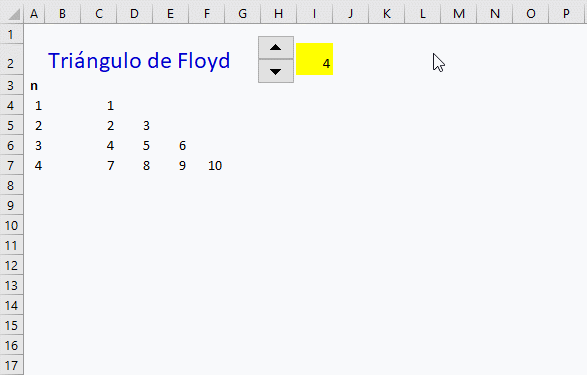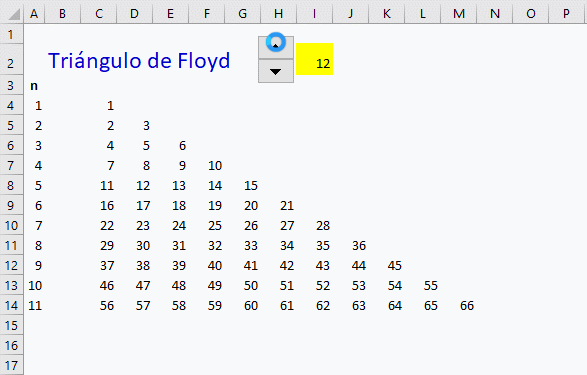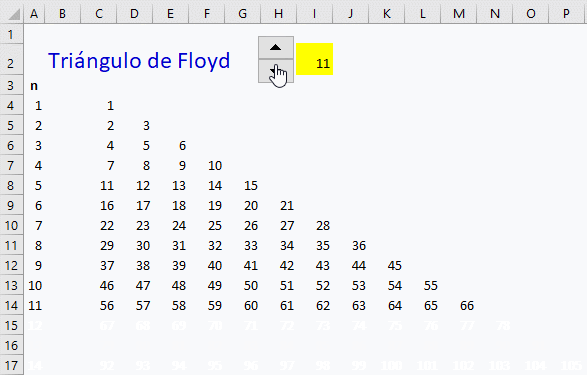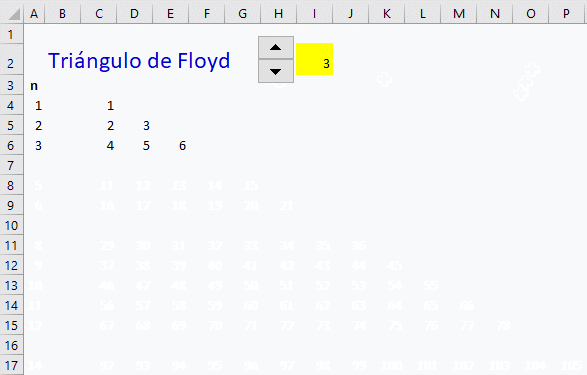
El triángulo de Floyd para cuatro filas es el siguiente.
Se construye con los números naturales en forma de triángulo rectángulo. Se suele utilizar como ejercicio para los que están aprendiendo a programar en un cierto lenguaje.
El triángulo de Floyd se resuelve con un algoritmo que ideó el Dr. Floyd, científico e informático que fue compañero de habitación de Carl Sagan cuando ambos estudiaban en la universidad.
Hoja 1
Resuelto usando fórmulas de Excel y sin usar macros.
La fórmula de la celda C5 calcula el máximo de la fila anterior para saber con qué número se ha de comenzar la fila actual.
=MAX(C4:P4)+1
La celda D5 suma 1 al valor previo y usa un condicional SI para saber hasta que valor se ha de continuar sumando 1.
=SI(CONTAR($C5:C5)<$A5;C5+1;"")
Hoja 2
También resuelve el triángulo con fórmulas y sin usar macros.
En este caso las celdas de la primera columna se obtienen con una fórmula que indica que nos da el último valor de la fila precedente y le suma 1. Se cumple que los últimos valores de cada fila son los llamados números triangulares, que se obtienen como n*(n+1)/2. Siendo n el número de fila.
En nuestro caso la celda C5 tiene la siguiente expresión.
=(A5*(A5-1)/2)+1
La celda D5 se calcula con la siguiente fórmula, que es igual a la empleada en la Hoja1.
=SI(CONTAR($C5:C5)<$A5;C5+1;"")
Hoja3
Se construye el triángulo de Floyd mediante macro.Sub Floyd1()
Dim n As Long, i As Long, j As Long, n_max As Long
Dim R As Range
Worksheets("Hoja3").Activate
Set R = Range("B3")
n_max = 24: j = 1
R.Offset(1, -1).Resize(n_max+2, n_max+2).ClearContents
For n = 1 To n_max
R.Offset(n, -1) = n 'imprimimos la columna A
For i = 1 To n 'i recorre los elementos de cada fila
R.Offset(n, i) = j 'imprimimos el valor de j en la celda que toca
j = j + 1 'j proporciona los números naturales correlativos
Next i
Next n
End Sub
Hoja4
Dada una fila n, podemos calcular el último valor de su fila usando los números triangulares que son los siguientes.- Para n=1 el número triangular es 1
- Para n=2 el número triangular es 3
- Para n=3 el número triangular es 6
- Para n=4 el número triangular es 10
- Para n=5 el número triangular es 15
A esos valores e le suma 1 para saber cuál es el primer valor de la fila siguiente.
Sub Floyd2()
Dim n As Long, i As Long, j As Long, n_max As Long
Dim R As Range
Worksheets("Hoja4").Activate
Set R = Range("B3")
n_max = 24
R.Offset(1, -1).Resize(n_max+2, n_max+2).ClearContents
For n = 1 To n_max
R.Offset(n, -1) = n
'primera columan del triángulo
R.Offset(n, 1) = (n * (n - 1) / 2) + 1
For i = 2 To n
R.Offset(n, i) = R.Offset(n, i - 1) + 1
Next i
Next n
End Sub
Hoja5
Una pequeña variante para poder elegir el número de filas desde un control numérico que se encuentra en la propia hoja de cálculo.
También está disponible en un lenguaje de programación que está muy de moda.