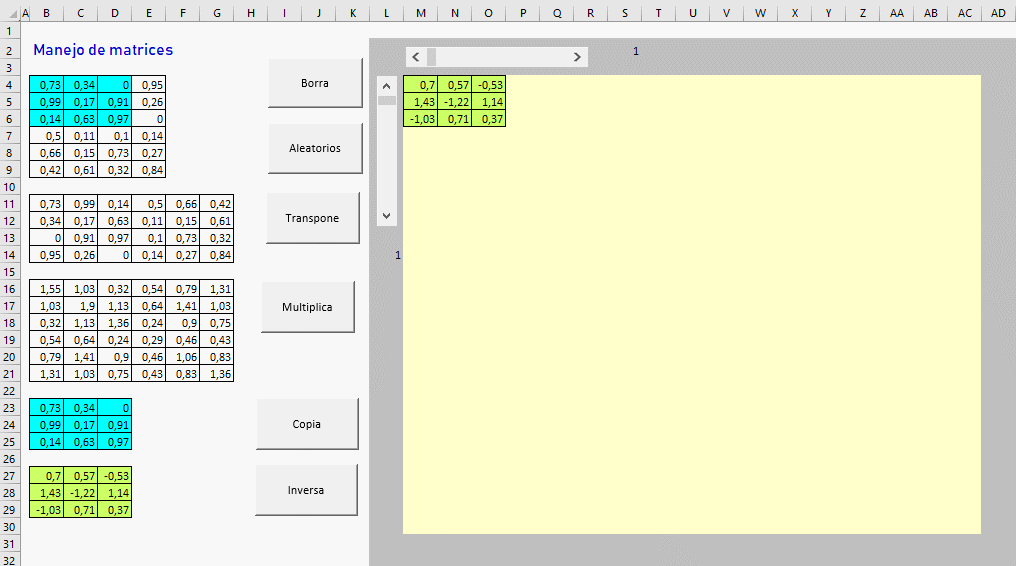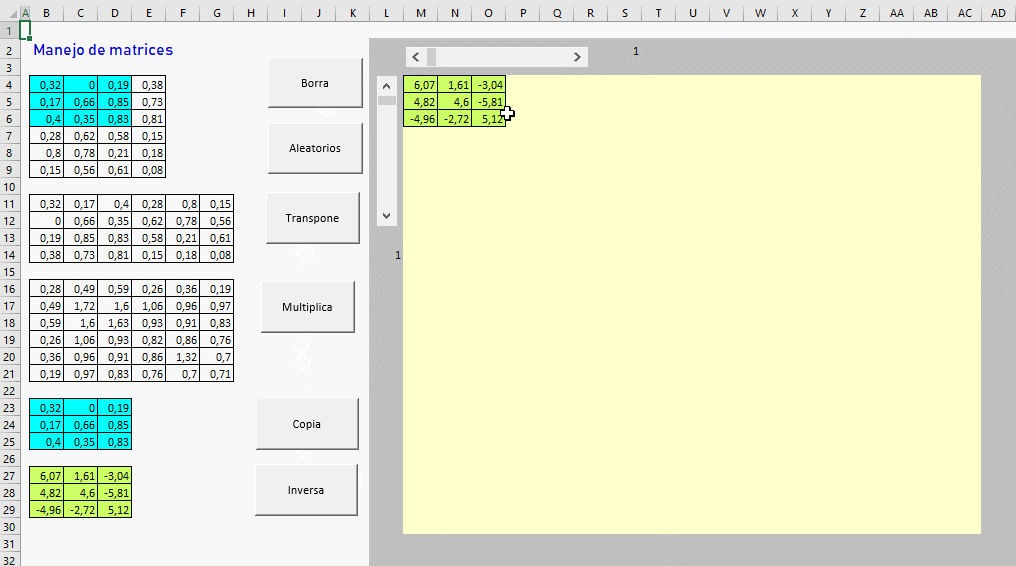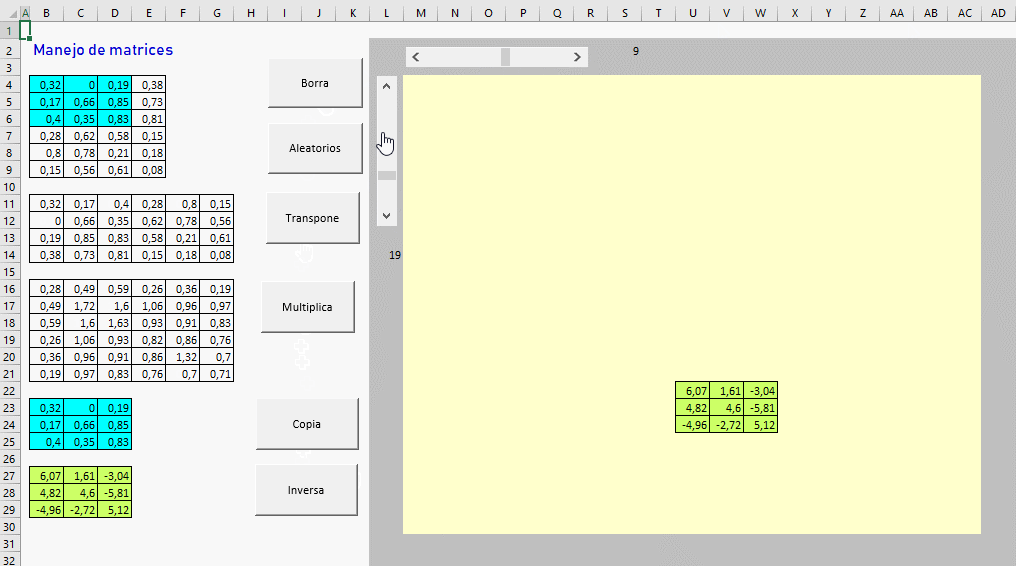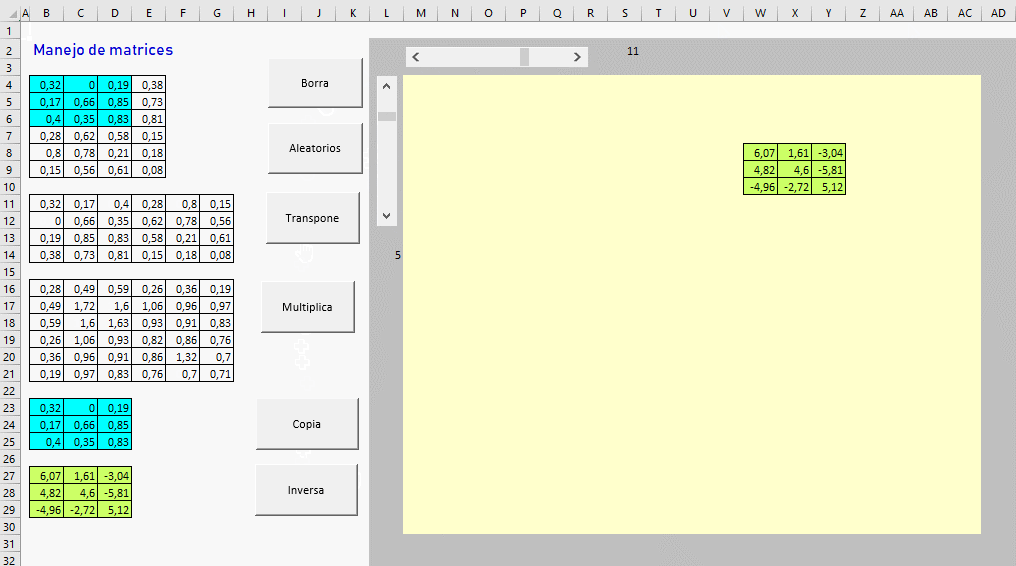
Vamos a trabajar con matrices en Excel programando en VBA (Visual Basic for Applications).
Lo interesante de este caso es ver que para dejar el contenido de una matriz en la hoja de cálculo lo que debemos hacer es lo que nos dice la intuición.
Rango = Matriz 'respetando las dimensionesOption Base 1 'Las matrices empiecen en 1 y no en 0
Sub manejaMatriz()
Dim A As Variant
Dim B As Variant
'para asignar un rango a una matriz
A = Range("B4:E9")
'para asignar una matriz a un rango
B = WorksheetFunction.Transpose(A)
'para imprimir una matriz en un rango
Range("B11:G14") = B
End Sub
Sub aleatorios()
Dim A(6, 4) As Double
Dim inicio As Range
Dim final As Range
Randomize 'para mejorar la aleatoriedad
For i = 1 To 6
For j = 1 To 4
'números aleatorios [0,1) a dos decimales
A(i, j) = Int(Rnd() * 100) / 100
Next j
Next i
Set inicio = Cells(4, "B")
Set final = Cells(9, "E")
Range(inicio, final) = A
End Sub
Sub multiplicaMatriz()
Dim A() As Variant
Dim B() As Variant
Dim C() As Variant
A = Range("B4:E9")
B = Range("B11:G14")
C = WorksheetFunction.MMult(A, B)
Range("B16:G21") = C
End Sub
Sub invierteMatriz()
Dim A() As Variant
A = Range("B23:D25")
Range("B27:D29") = WorksheetFunction.MInverse(A)
Range("B27:D29").Interior.Color = 6750156
Call extraeElementos
End Sub
Sub extraeElementos()
Dim A() As Variant
Dim origen As Range
Range("M4:AC30").Clear
Range("M4:AC30").Interior.Color = 13434879 'amarillo
Set origen = Range("L3")
A = Range("B27:D29")
fila = [L14]
columna = [S2]
For i = 1 To 3 'recorremos las 3 filas de la matriz
For j = 1 To 3 'recorremos las 3 columnas de A
With origen.Offset(fila + i - 1, columna + j - 1)
.Value = A(i, j)
.Borders(xlEdgeLeft).LineStyle = xlContinuous
.Borders(xlEdgeRight).LineStyle = xlContinuous
.Borders(xlEdgeTop).LineStyle = xlContinuous
.Borders(xlEdgeBottom).LineStyle = xlContinuous
End With
Next j
Next i
Range(origen.Offset(fila + i - 4, columna + j - 4), origen.Offset(fila + i - 2, columna + j - 2)).Interior.Color = 6750156
End Sub
Sub copia()
Dim A As Variant
A = Range("B4:D6")
Range("B23:D25") = A
Range("B4:D6,B23:D25").Interior.ColorIndex = 8
End Sub
Sub Borra()
Range("B4:AD32").ClearContents
[S2] = 1: [L14] = 1
Range("B4:G29").Interior.Pattern = xlNone
Range("M4:AC30").Clear
Range("M4:AC30").Interior.Color = 13434879 'amarillo
End Sub
También es interesante ver el pos siguiente.