Puede descargar el archivo
sumarsi.xlsx
La función SUMAR.SI nos permite hacer una suma condicional. Esto es, no suma todo el rango indicado sino únicamente las celdas del rango que cumplen el criterio que deseamos imponer.
La sintaxis de la formula es la siguiente.
=SUMAR.SI(rango, criterio, [rango_suma])
Veamos sus argumentos.
- rango: es el rango que se analiza en el argumento criterio
- criterio: es una igualdad o desigualdad que deben cumplir las celdas del rango especificado anteriormente
- [rango suma]: es un argumento optativo que en ocasiones se ha de utilizar y en otras no. Este argumento no se usa cuando el rango que deseamos sumar es el que se ha especificado en primer lugar. Si el rango especificado en primer lugar, que es el que cumple o no el criterio, no es el que deseamos sumar sino otro, se debe especificar en este tercer argumento ese otro rango que deseamos sumar.
Veamos los ejemplos contenidos en el archivo descargable indicados al inicio de este post.
Hoja1 Caso 1
Primero veamos el caso donde no se ha de utilizar el tercer argumento [Rango de suma] ya que deseamos sumar justo el rango que se usa al analizar el criterio.
Disponemos de una tabla con 20 ciudades donde figura el número de habitantes que tienen y el número de empresas de cierto sector radicadas en esa ciudad.
Deseamos conocer cuantos habitantes hay entre todas las ciudades siempre que estas tengan más de 700.000 habitantes. Para ello utilizamos la función siguiente que se encuentra en la celda H7.
=SUMAR.SI(Habitantes;">=700000")
Observe que hemos nombrado rangos que son los siguientes.
- Empresas =Hoja1!$D$5:$D$24
- Habitantes =Hoja1!$C$5:$C$24
- Población =Hoja1!$B$5:$B$24
Nota
Todos los datos de Habitantes y Empresas se generan con funciones aleatorias. De esta forma cada vez que se presiona la tecla F9 de recálculo manual, o bien, cada vez que se introduce un valor en una celda y se pulsa ENTER, lo que sucede es que se calcula toda la hoja, y por tanto los valores aleatorios cambian.
En este caso para los Habitantes hemos usado la función siguiente.
=ALEATORIO.ENTRE(50;1000)*1000
Hoja1 Caso 2
Ahora deseamos conocer el número de empresas que se encuentran radicadas en ciudades que tengan más de 700.000 habitantes.
Para ello utilizamos la formula siguiente que se encuentra en la celda H11.
=SUMAR.SI(Habitantes;">=700000";Empresas)
Observe que ahora ha sido necesario introducir el tercer argumento ya que no deseamos sumar habitantes sino empresas. Los habitantes se analizan en el criterio pero lo que deseamos es sumar número de empresas.
Nota
Para generar las Empresas hemos utilizado la inversa de la Normal.
=REDONDEAR(INV.NORM(PROMEDIO(ALEATORIO();ALEATORIO();ALEATORIO();ALEATORIO();ALEATORIO();ALEATORIO());C5/3000;C5/10000);0)
Hemos usado como probabilidad el promedio de seis valores aleatorios uniformes cero uno U[0,1] con la función ALEATORIO(). El motivo es que así obtenemos un valor aleatorio entre 0 y 1 pero que ya no es uniforme y se encuentra más centrado en la media que es 0,5, pero aún tiene suficiente dispersión. Si en lugar de seis valores aleatorios hubiéramos usado un gran número de ellos veríamos como se cumple el teorema central del límite, donde para infinitos sumandos el valor obtenido tiende a una normal.
Hoja2 Caso 1
Disponemos en la columna B de una serie de datos fijos. Son números que van del 100 al 1.000, en saltos de 100. Creamos un nombre de rango que se llama Datos que es rango B5:B14.
El el Caso 1 deseamos conocer la suma de los valores del rango Datos que sean <= 300. Esto lo calculamos en la celda F6 con la siguiente función.
=SUMAR.SI(Datos;"<=300")
En el primer argumento indicamos el rango Datos. Si no hubiéramos nombrado el rango también podríamos haber puesto simplemente B5:B14.
En el segundo argumento de la función indicamos el criterio, que ha de ir entre comillas. Como en este primer caso el valor de 300 es fijo, va dentro de las comillas: "<=300".
Hoja2 Caso 2
El el segundo caso no deseamos que el valor 300 sea fijo, por lo que creamos la celda amarilla para que el usuario pueda poner el valor que desee. En el ejemplo de la imagen anterior hemos puesto en la celda amarilla el valor 400, así pues, deseamos calcular la suma de los datos que sean menor o igual a 400. Pero ese valor de la celda amarilla puede variar por lo que debemos escribir el criterio usando el concatenador & y así poder unir "<=" con la celda amarilla que es E10.
La fórmula queda así:
=SUMAR.SI(Datos;"<="&E10)
Si prueba a usar como criterio la expresión "<=E10" verá que no funciona. Es imprescindible usar el concatenador & que nos permite unir cadenas alfanuméricas.
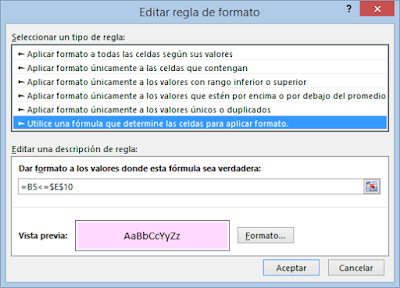
Formato condicional
El rango Datos marca con un color rosa las celdas que cumplan que son menores o iguales que el valore marcado en la celda E10 (amarilla).
Pruebe a cambiar el valor de la celda amarilla y verá como cambia el color de las celdas del rango Datos.
Para conseguir este formato condicional hemos usado la siguiente expresión aplicada a la celda B5.
=B5<=$E$10
Y luego hemos aplicado este formato a todo el rango Datos. Esto lo hemos conseguido con la brocha que nos permite copiar y pegar, formato.